3N-kinematische Konfigurationen

Aus verschiedenen Gründen werden im 3-Teilchen Aufbruch unterschiedliche ausgezeichnete kinematische Konfigurationen untersucht :

FSI (Final State Interaction)
QFS (Quasi Free Scattering)
COL (COLlinearity)
SST (Space STar)
SCRE (Symmetric Constant Relative Energy)
CPS (CoPlanar Star)

Die folgenden Konfigurationen beziehen sich auf die Reaktion ²H(p, pp)n mit der entsprechenden Kinematik und Notation. In einer Messung der Aufbruchsreaktion wird eine kinematische Kurve aufgenommen, von der aber nur ein Punkt der untersuchten kinem. Situation entspricht.

Bei koplanaren Meßgeometrien (FSI, QFS, COL) liegen die Impulse der eingehenden und auslaufenden Teilchen im Schwerpunktsystem in in einer Ebene.

1. FSI

Final State Interaction (Endzustands Wechselwirkung)

Die FSI-Konfiguration ergibt sich aus einer verschwindendenden Relativ-Energie im Schwerpunktsystem zwischen den zwei Nukleonen des Targets im Ausgangskanal

E_{i , CM} = E_{j , CM} , bzw. E_{ij, CM} = 0

mit

i, j = {3, 4, 5} , und i j

Fig.1.1:

Impulskonfiguration der pn-FSI im Schwerpunkt-System

In der Reaktion ²H(p,pp)n können folgende FSI-Punkte untersucht werden :

n₅ p₃-FSI , p₄ n₅-FSI , p₃ p₄-FSI

Die beiden np-FSI Konfigurationen sind symmetrisch zu E₃ = E₄ .

Die FSI ist ein dominierender Prozeß im 3-Teilchenaufbruch. Der Wirkungsquerschnitt in der FSI-Konfiguration hängt stark von der Wechselwirkung im 2-Teilchen Subsystem ab. Einzig im FSI-Punkt haben beide Teilchen des Targets eine verschwindende Relativ-Energie. Im FSI-Ausläufer übernimmt das Projektil den Platz eines Teilchens aus dem Target.
Die deutliche Überhöhung im FSI-Punkt wird durch das Auftreten einer Polstelle in der Singulett-T-Matrix erklärt [Glö83a].

Fig. 1.2

Wirkungsquerschnitt der FSI-Konfiguration
bei E_p = 19 MeV aus [Pat96]

2. QFS

Quasi Free Scattering (Quasi Freie Streuung)

In der QFS wird die 3-Teilchen-Aufbruch Reaktion auf eine quasi inelastische 2-Teilchen Streuung reduziert. Eines der Nukleonen aus dem Deuteron nimmt an der Reaktion nicht Teil. Der Aufbruch findet statt, jedoch beobachtet ein Nukleon aus dem Deuteron die Reaktion nur und bleibt ohne Impuls im Target zurück.

E_{(4,5), lab} = 0

Das unbeteiligte Teilchen wird auch als Spectator (Beobachter) bezeichnet. Der QFS-Punkt wird durch gleiche Energie beider auslaufender Teilchen charakterisiert.

E_{3, lab} = E_{(5,4), lab}

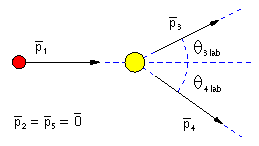
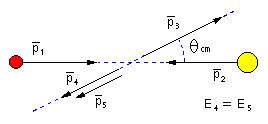
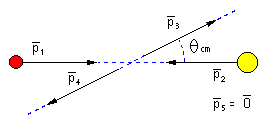
Fig.2.1

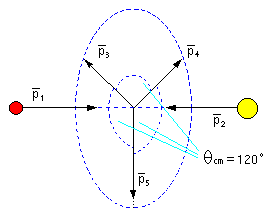
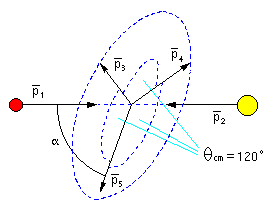
Impulskonfiguration der pp-QFS im Labor-System

In der Reaktion ²H(p, pp)n sind somit die Messung folgender QFS-Punkte möglich :

p₃ p₄-QFS , p₃ n₅-QFS

Da der Spectator die Reaktion nur beobachten soll, wird zumeist dem Neutron, wegen der Ladungsneutralität, diese Rolle zugedacht. Die pp-QFS entspricht somit quasi der Reaktion p(p, p)p* mit dem Q-Wert des Deuteron-Aufbruchs (Q = -2.224 MeV).

Der Wirkungsquerschnitt in der QFS-Konfiguration zeigt einen breiten Peak um den QFS-Punkt. Die Breite des Peaks ist auf die Impulsverteilung der Teilchen im Target zuückzuführen. Das im Targetort verbleibende Teilchen hat nach der Reaktion keinen Impuls mehr. Der Impuls des zurückbleibenden Teilchens wird vom auslaufenden Teilchen mitgenommen. Dies führt zu einer statistischen Verbreiterung des QFS-Punktes auf der kinematischen Kurve.
Die QFS besitzt ähnlich der FSI einen dominanten Reaktionsmechanismus, der aber durch die Impulsverschmierung weniger stark zu beobachten ist, als in der FSI.

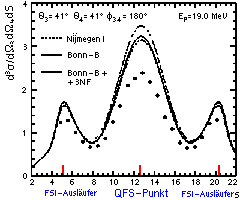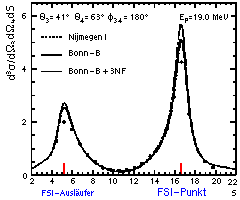
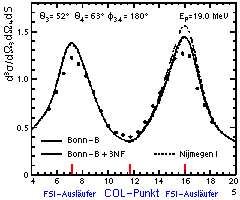
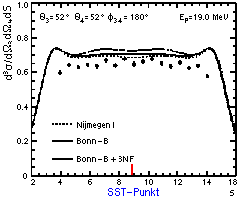
Fig. 2.2

Wirkungsquerschnitt der QFS-Konfiguration
bei E_p = 19 MeV aus [Pat96]

3. COL

Collineratity (Kollinearität)

Die Kollinearität wird dadurch gekenzeichnet, das ein Teilchen im Schwerpunktsystem seine Energie verliert.

E_{(4,5), CM} = 0

Die Ejektile liegen im Schwerpunktsystem auf einer Geraden. Im COL-Punkt haben beide auslaufenden Teilchen gleiche Energie.

E_{3, CM} = E_{(5,4), CM}

Hier wirken die 2-Körper Kräfte der beiden auslaufenden Teilchen entgegengesetzt gleich groß auf das ruhende Teilchen. Somit heben sich die 2-Körper Kräfte auf und eine 3-Körper Kraft sollte genau beobachtet werden können [Mei84].

Fig.3.1

Impulskonfiguration der COL im Schwerpunkt-System

In der Reaktion ²H(p, pp)n sind somit die Messung folgender COL-Punkte möglich :

p₃ p₄-COL , p₃ n₅-COL

Zur Verkleinerung der 2-Körper Kräfte, aber auch wegen der Ladungsneutralität, wird zumeist in der pp-COL Konfiguration gemessen.

Obwohl die COL-Konfiguration eine coplanare Konfiguration ist und wie die Übertragung der QFS in das Schwerpunktsystem aussieht, ist sie kein dominater Reaktionsmechanismus. Am deutlichsten sind die beiden FSI-Ausläufer zu messen, zwischen denen der COL-Punkt zu liegen kommt.

Wirkungsquerschnitt in der COL-Konfiguration

Fig. 3.2

Wirkungsquerschnitt der COL-Konfiguration
bei E_p = 19 MeV aus [Pat96]

4. SST

Space Star (Raumstern)

In der SST-Konfiguration liegen alle Impulse der Ejektile im Schwerpunktsystem in einer Ebene, die ihrerseits senkrecht zu den Impulsen von Projektil und Target steht. Alle drei ausgehenden Teilchen bilden einen symmetrischen Raumstern im Schwerpunktsystem. Die Winkel zwischen den Impulsen betragen 120^o Grad.

Der SST-Punkt wird durch gleiche Energie aller drei auslaufender Teilchen charakterisiert.

E_{3, CM} = E_{4, CM} = E_{5, CM}

Die Messung der SST-Konfiguration ist besonders interessant, da realistische NN-Kräfte und die Tucson-Melbourne 3-Nukleon Kraft keine vollständige Beschreibung der Physik in dieser Konfiguration wiedergeben [How98].

Fig.4.1

Impulskonfiguration des SST im Schwerpunkt-System

In der Reaktion ²H(p,pp)n können folgende SST-Punkte untersucht werden :

n₅ p₃-SST , p₄ n₅-SST , p₃ p₄-SST

Im Allgemeinen wird hiervon aus Symmetriegründen (gleiche Massen) und Ladungsunabhängigkeit der pp-SST untersucht.

Der SST-Punkt liegt kinematisch weit entfernt von konkurrierenden dominanten 2-Teilcheneffekten wie FSI oder QFS. Im Wirkungsquerschnitt zeigt sich ein breites Plateau, auf dem der SST-Punkt sitzt.

Abschätzungen mit vereinfachten NN-Kräften [Alt94] zeigen einen kleineren Wirkungsquerschnitt für den pd-Aufbruch gegenüber dem nd-Aufbruch, der auch im Experiment beobachtet wird. Im pd-Aufbruch zeigt sich aber dennoch eine Diskrepanz von 20 % zwischen Daten und Theorie [Str89].

Wirkungsquerschnitt in der SST-Konfiguration

Fig. 4.2

Wirkungsquerschnitt der SST-Konfiguration
bei E_p = 19 MeV aus [Pat96]

5. SCRE

Symmetric Constant Relative Energy

Die SCRE-Konfiguration entspricht beim Winkel = 90^o der SST-Konfiguration.
Die Ebene der drei auslaufenden Teilchen im Schwerpunktsystem ist um einen Winkel gekippt. Der Winkel ist gleich dem Winkel zwischen Projektil und unbeobachtetem Ejektil im Schwerpunktsystem.
Mit = 0^o geht die SCRE-Konfiguration in den coplanaren Stern (coplanar Star, CPS) über.

Im SCRE-Punkt haben wie im SST-Punkt alle drei Ejektile gleiche Energie.

Diese Konfiguraton wurde erstmals in Ref. [Jai73] zur Untersuchung kleiner Effekte in Verbindung mit off-shell Anteilen in der NN-Wechselwirkung oder 3-Körper Kraft vorgeschlagen.

Fig.5.1

Impulskonfiguration der SCRE im Schwerpunkt-System

Return to Physics-Page